傅里叶级数

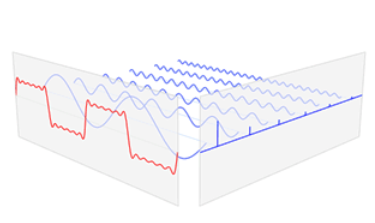
任何周期函数都可以看昨是不同振幅，不同相位正弦波的叠加。

$$ f\left( t \right) =\frac{a_0}{2}+\sum_{k=-\infty}^{\infty}{a_k\sin \left( kw_0t+\varphi _k \right)} \\ f\left( t \right) =\frac{a_0}{2}+\sum_{k=-\infty}^{\infty}{\left[ a_k\sin \left( kw_0t \right) +b_k\cos \left( kw_0t \right) \right]} \\ f\left( t \right) =\frac{a_0}{2}+\sum_{k=-\infty}^{\infty}{a_ke^{jkw_0t}} $$

其中，$w_0$是基波的角速度

傅里叶变换

由于一个任意的函数可以看做一个周期为无限大的周期函数，所以任意函数都可以转换为傅里叶级数，对该傅里叶级数与一个正交基做内积并在整个时域上积分。
此时，若某频率的分量为0，则内积为0，反之若某频率分量不为0，则内积不为0。

$$ F(w)=\int\limits_{-\infty}^{+\infty}{f\left( t \right) e^{-jwt}dt} \\ F(f)=\int\limits_{-\infty}^{+\infty}{f\left( t \right) e^{-2\pi ift}dt} $$

注意上式的$f$和$w$是频谱图中的变量。

图形上的另一种直观理解

$$ F(f)=\int\limits_{-\infty}^{+\infty}{f\left( t \right) e^{-2\pi ift}dt} $$

将该公式换一种理解，该公式的意义在于将$f(t)$在复平面上缠绕，不同的频率$f$对应不同的缠绕速度。缠绕后，若该图形的质点偏移坐标原点很多，则说明该频率是$f(t)$的一个频率分量。