向量数学

点积

该点积是矢量数学最重要的概念之一，但经常被误解。点积是对两个向量返回标量的运算。与既包含幅度又包含方向的向量不同，标量值仅包含幅度。

$$ A \cdot B = |A| |B| \cdot cos\theta $$

var c = a.dot(b)
var d = b.dot(a) # These are equivalent.

叉积

像点积一样，叉积是对两个向量的运算。但是，叉积的结果是一个向量，向量的方向垂直于两者。其大小取决于它们的相对角度。如果两个向量平行，则其叉积的结果将为空向量。

var c = a.cross(b)

Transform2D

简单来说，transform 属性是为了方便运动控制。和position等价的另一套控制运动位置的属性。
（在这里总结一下，这里我会了三种控制运动的手段。第一种通过设定position属性 ，第二种通过设定transform属性，第三种使用velocity然后通过内置 move_and_slide() 来自动控制。）

属性：
Vector2 x [默认： Vector2( 1, 0 )]
Vector2 y [默认： Vector2( 0, 1 )]
Vector2 origin [默认： Vector2( 0, 0 )]

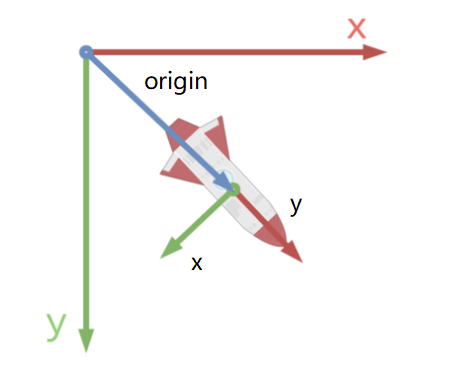
x和y决定node2D的旋转(rotation)，缩放(scale)，和剪切。
origin决定初始位置，等价于position

参考链接：http://kidscancode.org/godot_recipes/math/transforms/
参考链接2：https://docs.godotengine.org/en/latest/tutorials/math/matrices_and_transforms.html